【教師なし学習】k-means(k平均法)により似たデータをクラスタリング(グループ化)する

前提知識
教師なし学習とは?
教師なし学習とは、ラベル(正解)のない学習のことである。
例えば、犬猫の画像を用意して、それぞれ個々の画像に犬と猫のラベル(正解)を与えた上で学習させる方法を教師あり学習という。
一方で、教師なし学習の場合、犬と猫の画像をまとめて与えるだけで、犬や猫のラベル(正解)は学習に含ませない。
この教師なし学習のメリットは、事前にラベルを用意する必要がないということ。
例えば、ラベリングにコストのかかる
- ラベリングに専門知識が必要なデータ
- データ量が膨大
などの学習に対して有効である。
分類問題とクラスタリングの違いは?
教師あり学習の中には、回帰問題と分類問題の2つがある。
- 回帰問題は、価格や数量などの数値を予測する問題である。
- 分類問題は、カテゴリや品種などのグループを予測する問題である。
クラスタリングとは、教師なし学習に当たる。
事前のラベリング情報が無いので、AIが自分で分類していく。これは正確な分類とは異なるため、クラスタリングという。
- 分類問題は教師あり学習の一種
- クラスタリングは教師なし学習の一種
数値を予測するわけではない点では共通しているが、分類問題とクラスタリングは教師あり・なしという点で異なる。
今回のk平均法は、クラスタリング(教師なし学習) に該当する。
k-means(k平均法) とは?
k平均法は、データをクラスタリング(グループ化)する、教師なし学習の一種である。
k-NN(k近傍法)とk-means(k平均法)の違いとは?
似た言葉にk近傍法というものがある。k近傍法は教師あり学習であり、事前にラベルを渡すという点で、k平均法とは異なる。
k近傍法は、ラベリングされたデータから近いものを取り出すので、近傍という。主に分類問題で活用される。
一方、k平均法は、ラベリングされていないため、平均を取り出す必要があることから、平均という。主にクラスタリングで活用される。
ちなみにmeansは平均を意味する言葉である。
k-means(k平均法)により、何ができるのか?
k平均法は、教師なし学習のクラスタリングができる。
これはつまり、膨大な量のデータから似た情報をグループ化できるということ。
- SNSから、ユーザーの興味のある情報をまとめ、DMを送る
- 商品の閲覧履歴から、ユーザーの興味のある商品をまとめ、セールする
などができる。
いわゆる、リコメンド機能の実装ができる。
Amazonなどの大手ECのリコメンド機能は、このk平均法から更に学習させ、より的確なリコメンドが実現できている。
実際にk平均法のコードを組む
全体の流れ
- データを可視化する
- Kmeans でクラスタリング、学習と予測をする
- 整形して正解と比較をする
環境構築とコード
seabornとscikit-learnとpandasとmatplotlibをインストールしておく。
contourpy==1.3.2
cycler==0.12.1
fonttools==4.58.0
joblib==1.5.1
kiwisolver==1.4.8
matplotlib==3.10.3
numpy==2.2.6
packaging==25.0
pandas==2.2.3
pillow==11.2.1
pyparsing==3.2.3
python-dateutil==2.9.0.post0
pytz==2025.2
scikit-learn==1.6.1
scipy==1.15.3
seaborn==0.13.2
six==1.17.0
threadpoolctl==3.6.0
tzdata==2025.2
import pandas as pd
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
iris = load_iris()
# データの形状は (150 , 4) 変数は4つでサンプルのデータは150件。
print( iris.data.shape )
# 変数の名前 4つ ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)'] sepalはがく petalは花びら
# print( iris.feature_names )
# ラベルの名前(アイリスの品種) 3つ ['setosa' 'versicolor' 'virginica']
# print( iris.target_names )
# 変数の値 と ラベルの値
# print(iris.data)
# print(iris.target)
# 今回はクラスタリング(教師なし学習のk平均法)を使うため、iris.target は使わず、iris.target のみで学習をする。
df_iris = pd.DataFrame(iris.data, columns=iris.feature_names )
print(df_iris)
# データの全体像把握のため、平均値、最大値、最小値、を表示する。
print( df_iris.describe() )
# 上記データをグラフ化させる
import seaborn as sns
# sns.pairplot(df_iris)
# plt.show()
# ※: このグラフからわかること
# どの品種でも、petal(花びら) のwidth とlength は比例している。 petalのwidthが大きければlength も大きくなる。
# 一方、sepal(がく)のwidthとlengthは比例しているというわけではない。
# ===================== クラスタリング ===============================================================
# クラスタリングをする。
# 今回の分類品種は3種類なので、クラスタ数は3を指定する。
from sklearn.cluster import KMeans
# クラスタ数は3 ランスシードは0 クラスタセンター(クラスタの中心)の初期化はランダム
model = KMeans(n_clusters=3, random_state=0, init="random")
cls_data = df_iris.copy()
# k平均法で学習
model.fit(cls_data)
# k平均法で予測する
cluster_results = model.predict(cls_data)
# クラスタ番号( 0,1,2 )が割り振られている。
print( cluster_results )
# 結果をグラフで可視化すると、距離をベースにグループが作られていることがわかる。
cls_data["cluster"] = cluster_results
# sns.pairplot(cls_data, hue="cluster")
# plt.show()
# クラスタの中心(クラスタセンター)を確認する。
cluster_center = pd.DataFrame(model.cluster_centers_)
cluster_center.columns = cls_data.columns[:4]
print(cluster_center)
# クラスタセンターをグラフ化させる
# 花びらの大きさをどのように分類したのか確認するため、 sepalを指定する。
# plt.scatter(
# cls_data['sepal length (cm)'],
# cls_data['sepal width (cm)'],
# c=cls_data["cluster"],
# )
# plt.xlabel('sepal length (cm)')
# plt.ylabel('sepal width (cm)')
# plt.scatter(
# cluster_center['sepal length (cm)'],
# cluster_center['sepal width (cm)'],
# marker="*",
# color="red"
# )
# plt.show()
# クラスタリング結果と正解データと比較をする。
# その方法として、グループごとに平均を算出。正解のデータのグループごとの平均と比較をする。
print( cls_data.groupby("cluster").mean().round(2) )
# クラスタリングした結果(データフレーム)に、正解のiris.targetの値を加える
cls_data["target"] = iris.target
# わかりやすくするため、正解の結果に名前を与える。
# TIPS:数値型のデータフレーム(np配列)の値に対して、直に文字列型を与えると警告になるため、まずは文字列に変換する。
cls_data["target"] = cls_data["target"].astype(str)
# ['setosa' 'versicolor' 'virginica'] の順なのでインデックス番号に合わせて名前を与える。
cls_data.loc[cls_data["target"] == "0", "target"] = 'setosa'
cls_data.loc[cls_data["target"] == "1", "target"] = 'versicolor'
cls_data.loc[cls_data["target"] == "2", "target"] = 'virginica'
# k平均法の予測したクラスタリング番号と正解のインデックス番号の順番が異なるが、正解とほぼ同じようにクラスタリングができている
print(cls_data.groupby("target").mean().round(2))
【解説1】データの可視化
以下のコードは、scikit-learnのアイリスのデータからグラフを作っている。
import pandas as pd
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
iris = load_iris()
# データの形状は (150 , 4) 変数は4つでサンプルのデータは150件。
print( iris.data.shape )
# 変数の名前 4つ ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)'] sepalはがく petalは花びら
print( iris.feature_names )
# ラベルの名前(アイリスの品種) 3つ ['setosa' 'versicolor' 'virginica']
print( iris.target_names )
# 変数の値 と ラベルの値
print(iris.data)
print(iris.target)
# 今回はクラスタリング(教師なし学習のk平均法)を使うため、iris.target は使わず、iris.target のみで学習をする。
df_iris = pd.DataFrame(iris.data, columns=iris.feature_names )
print(df_iris)
# データの全体像把握のため、平均値、最大値、最小値、を表示する。
print( df_iris.describe() )
# 上記データをグラフ化させる
import seaborn as sns
sns.pairplot(df_iris)
plt.show()
結果、以下のグラフが表示される。
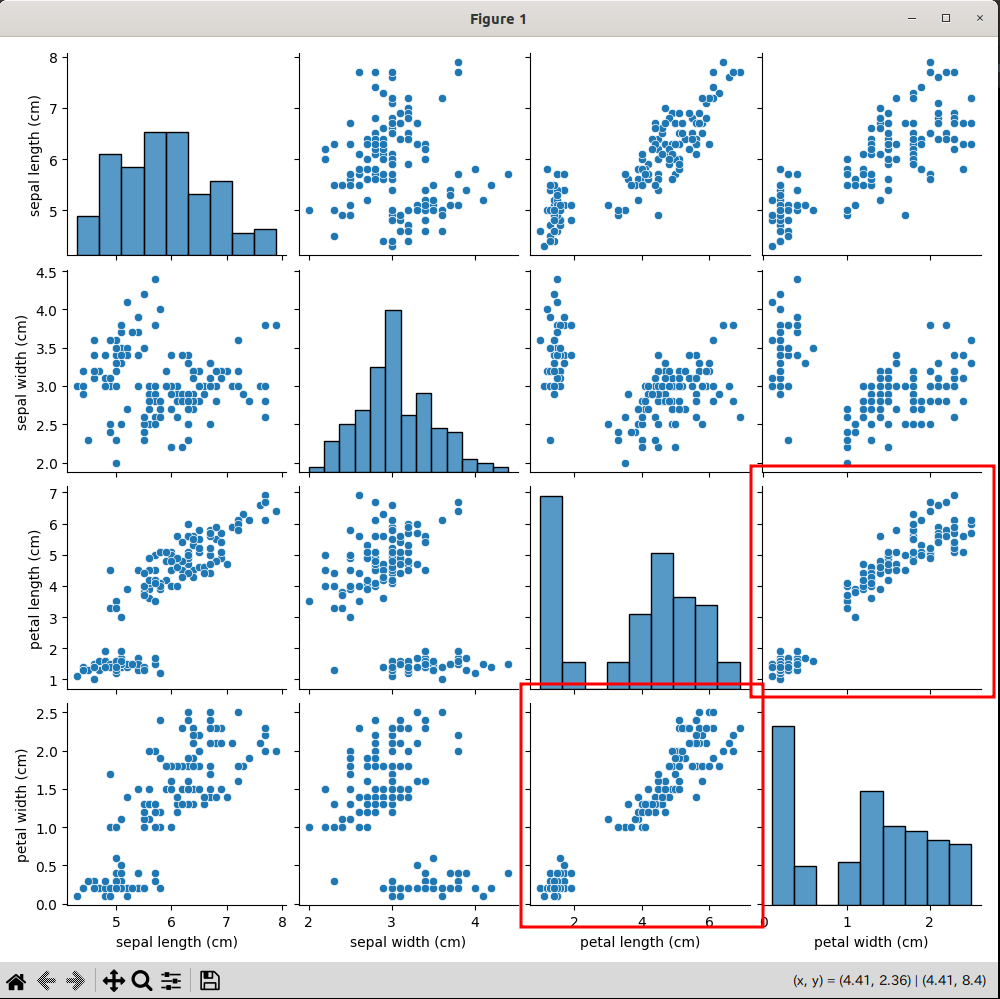
注目するべきは、右下の赤枠2つ。
petal(花びら)のwidthとheight は、すべての品種において比例関係にあることがわかる。
このように、データが視覚的にきれいに分布しているものの場合、k平均法による分類がしやすい。
【補足】k平均法で分類しやすいデータ、分類しにくいデータ
分類しやすいデータは
- データが線形に分離可能
- 各クラスタが等間隔で分布している
- 各クラスタのサイズが均等
などがある。つまり、先のグラフの赤枠2つは、直線を引いてデータを分類することが可能。(データの集合の中心を基準に分離できる)
一方で、k平均法で分類しにくいデータは
- データが非線形な分布
- 分布密度が極端に違う
- 変数が比例していない
などがある。つまり、グラフで線を引いて分類できないようなデータは、k平均法での分類が難しい。(データの集合の中心を基準に分離できない)
【解説2】k平均法でクラスタリングし、学習・予測をする
今回扱うデータがk平均法による分類(クラスタリング)が有効であることがわかったため、学習と予測をする。
# 今回の分類品種は3種類なので、クラスタ数は3を指定する。
from sklearn.cluster import KMeans
# クラスタ数は3 乱数のシードは0 クラスタセンター(クラスタの中心)の初期化はランダム
model = KMeans(n_clusters=3, random_state=0, init="random")
cls_data = df_iris.copy()
# k平均法で学習
model.fit(cls_data)
# k平均法で予測する
cluster_results = model.predict(cls_data)
# クラスタ番号( 0,1,2 )が割り振られている。
print( cluster_results )
# 結果をグラフで可視化すると、距離をベースにグループが作られていることがわかる。
cls_data["cluster"] = cluster_results
sns.pairplot(cls_data, hue="cluster")
plt.show()
# クラスタの中心(クラスタセンター)を確認する。
cluster_center = pd.DataFrame(model.cluster_centers_)
cluster_center.columns = cls_data.columns[:4]
print(cluster_center)
# クラスタセンターをグラフ化させる
# 花びらの大きさをどのように分類したのか確認するため、 sepalを指定する。
plt.scatter(
cls_data['sepal length (cm)'],
cls_data['sepal width (cm)'],
c=cls_data["cluster"],
)
plt.xlabel('sepal length (cm)')
plt.ylabel('sepal width (cm)')
plt.scatter(
cluster_center['sepal length (cm)'],
cluster_center['sepal width (cm)'],
marker="*",
color="red"
)
plt.show()
今回、分類する品種は3種類のため、n_cluster には3を指定する。
from sklearn.cluster import KMeans
model = KMeans(n_clusters=3, random_state=0, init="random")
init="random" はクラスタの初期中心をランダムに選ぶ方法
random_state は ランダム処理の再現性を保証するためのシード値。実験・デバッグ中などで結果に再現性が欲しい場合に、任意の値を指定する。
通常、クラスタの初期中心をランダムに選ぶ場合、random_stateも同時に指定をするのが定石。
こうして、k平均法によって学習・予測した結果を、グラフで可視化したものが下記。
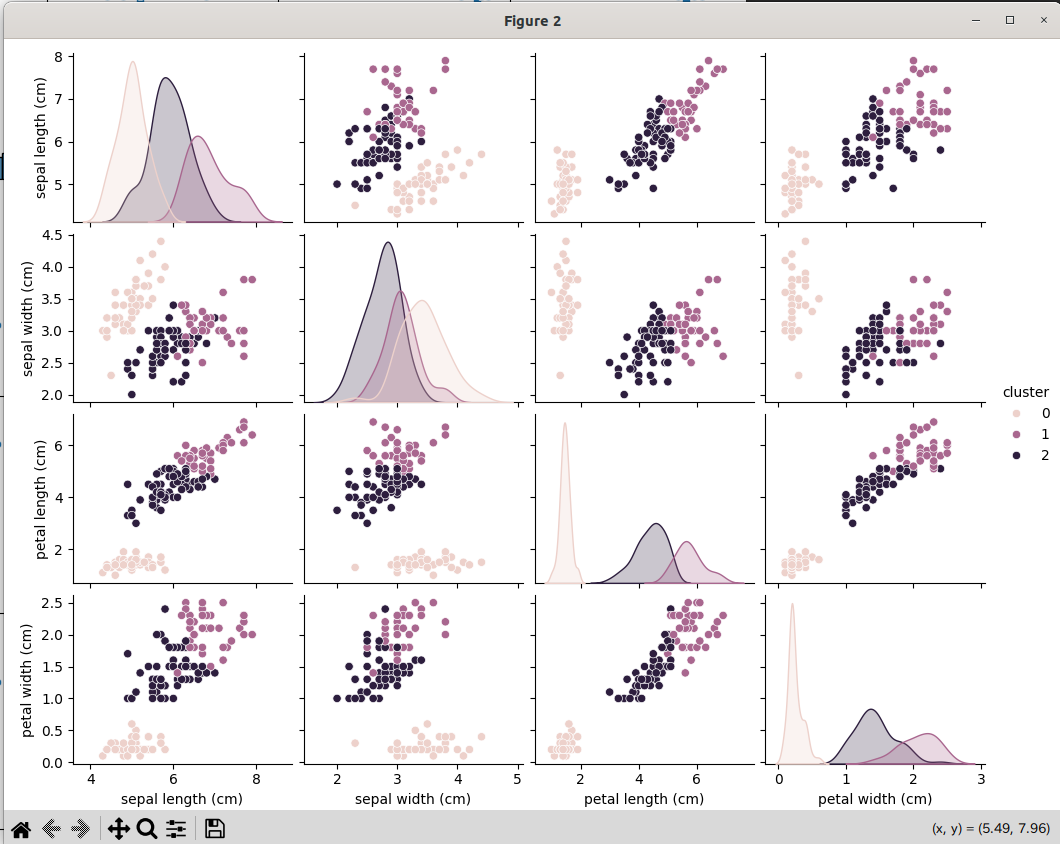
ここから、一部のグラフ(sepal length (cm)とsepal width (cm))を取り出し、クラスタの中心を可視化させる。
これで、k平均法がどのように分類をしたのかがわかる。
以下で、がくの大きさのグラフから、クラスタの中心を表現している。
# クラスタの中心(クラスタセンター)を確認する。
cluster_center = pd.DataFrame(model.cluster_centers_)
cluster_center.columns = cls_data.columns[:4]
print(cluster_center)
# クラスタセンターをグラフ化させる
# 花びらの大きさをどのように分類したのか確認するため、 sepalを指定する。
plt.scatter(
cls_data['sepal length (cm)'],
cls_data['sepal width (cm)'],
c=cls_data["cluster"],
)
plt.xlabel('sepal length (cm)')
plt.ylabel('sepal width (cm)')
plt.scatter(
cluster_center['sepal length (cm)'],
cluster_center['sepal width (cm)'],
marker="*",
color="red"
)
plt.show()
学習と予測をしたモデルには、クラスタの中心(.cluster_centers_)が記録される。
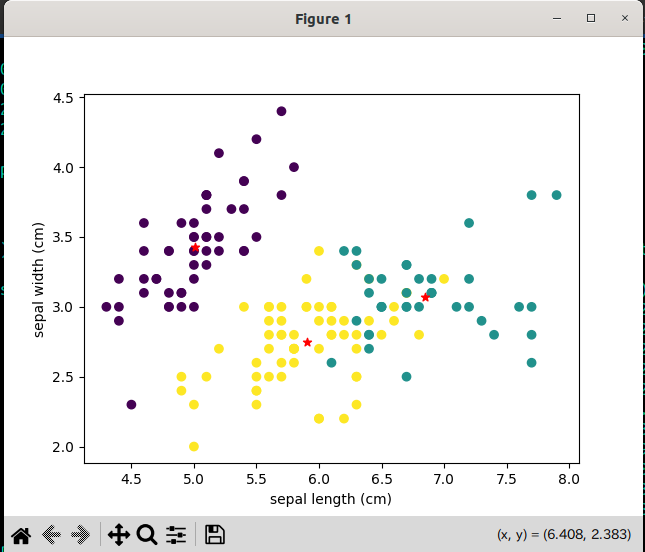
【補足1】クラスタリングの流れ
クラスタリングではデータの集合の中心を取り決める必要がある。
そこで、まずは初期中心位置をランダムに設定する。そして、徐々に正確な中心に寄せていく。
ただし、その初期中心位置を実行するたびに変化しているようでは、正確な中心位置に寄せていく過程で再現性がなくなる。
だから、初期中心位置の乱数シードを指定し、再現性を保つようにしている。
よって、
random_state=0 , init="random"
という引数になる。
【補足2】分類する数がわからない場合は、エルボー法を使う
今回は品種が3種類と事前にわかっているため、分類する数に3を指定した。
しかし分類する数が事前にわかっているケースばかりではない。
そういうときは、エルボー法を使って最適な分類数 を算出する。
エルボー法はk平均法を何度も繰り返し、分類数を増やしていく。その過程で分類の精度が改善できなくなった時、その分類数で打ち切る。
これにより最適な分類数を算出できる。
【解説3】予測と正解と照らし合わせる
# クラスタリング結果と正解データと比較をする。
# その方法として、グループごとに平均を算出。正解のデータのグループごとの平均と比較をする。
print( cls_data.groupby("cluster").mean().round(2) )
# クラスタリングした結果(データフレーム)に、正解のiris.targetの値を加える
cls_data["target"] = iris.target
# わかりやすくするため、正解の結果に名前を与える。
# TIPS:数値型のデータフレーム(np配列)の値に対して、直に文字列型を与えると警告になるため、まずは文字列に変換する。
cls_data["target"] = cls_data["target"].astype(str)
# ['setosa' 'versicolor' 'virginica'] の順なのでインデックス番号に合わせて名前を与える。
cls_data.loc[cls_data["target"] == "0", "target"] = 'setosa'
cls_data.loc[cls_data["target"] == "1", "target"] = 'versicolor'
cls_data.loc[cls_data["target"] == "2", "target"] = 'virginica'
# k平均法の予測したクラスタリング番号と正解のインデックス番号の順番が異なるが、正解とほぼ同じようにクラスタリングができている
print(cls_data.groupby("target").mean().round(2))
予測結果のラベルとそれぞれの変数の平均を表示している。
print( cls_data.groupby("cluster").mean().round(2) )
ラベルには0,1,2と表示しているが、正解ラベルの0,1,2と一致しているわけではない点に注意。
続いて、正解ラベルとそれぞれの変数の平均を表示している。
cls_data["target"] = cls_data["target"].astype(str)
cls_data.loc[cls_data["target"] == "0", "target"] = 'setosa'
cls_data.loc[cls_data["target"] == "1", "target"] = 'versicolor'
cls_data.loc[cls_data["target"] == "2", "target"] = 'virginica'
print(cls_data.groupby("target").mean().round(2))
こちらは、インデックス番号をそのまま表示すると、予測のラベルと混同しかねないので、品種を割り当てている。
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)
cluster
0 5.01 3.43 1.46 0.25
1 6.85 3.07 5.74 2.07
2 5.90 2.75 4.39 1.43
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm) cluster
target
setosa 5.01 3.43 1.46 0.25 0.00
versicolor 5.94 2.77 4.26 1.33 1.96
virginica 6.59 2.97 5.55 2.03 1.28
このように出力される。
こうしてみると、
- 予測の0はsetosa
- 予測の1はvirginica
- 予測の2はversicolor
のデータと近いことがわかる。適切にクラスタリングができているようだ。